By Patrick Hunt –
According to 17th century German mathematician Gottfried Leibniz, “Music is a secret exercise in the arithmetic of the soul.” That music and mathematics are deeply wedded needs no explanation, since “Music is mathematics you can hear” [1] If anyone could hear the mathematics of music, it was Bach. Sometimes Bach may appear to hide connotations in his music in steganographic symbolic motifs, that is, playing with ideas or names more or less in plain sight, not unusual for a genius of his musical erudition and in no way reducing his sublime music to programmatic effect. A previous article in this series, “Mozart and Mathematics”, explored similar periodicity and symmetry in Mozart’s music and the “Mozart Effect” on how such mathematically-ordered music may enhance problem solving and temporal spatial reasoning. [2]
Was Bach directly interested in numbers beyond the pure mathematics of music? Much ink has been used to show Bach as a regular practitioner of musical gematria and hidden number symbolism, possibly in keeping with the times in which he lived, the age just after Athanasius Kircher (1602-80) when speculation filled many gaps in knowledge.
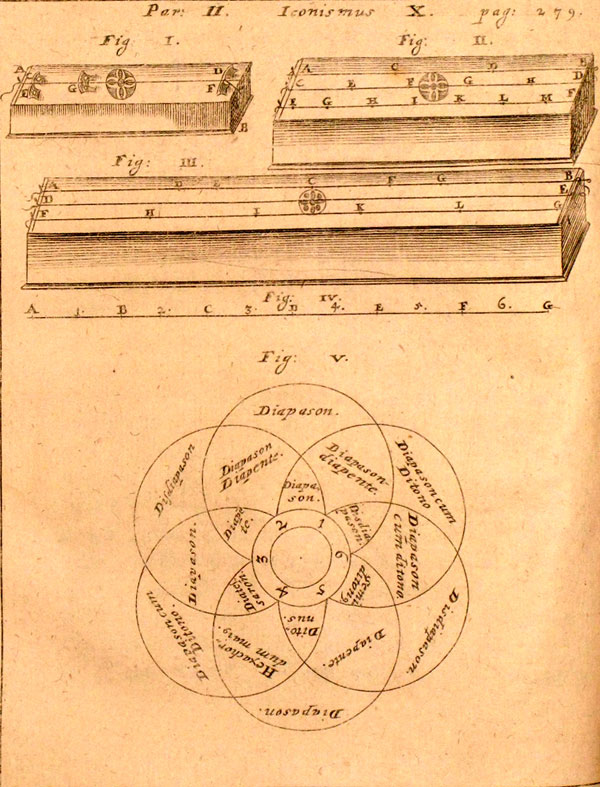
One of Kircher’s students at Warzburg, Gaspar Schott (1608-60), wrote about music relative to universal harmony as well as musical mathematics and other topics, including musical steganography. The page of diagrams below from one of Schott’s works on the mathematics of music shows in figs. I-IV the mathematical basis for the major scale dividing the monochord string in up to six parts and fig. V explains the intervals through ratios using Greek interval names.[3]
While so many of the claims of Bach as a “Caballistic” gematrist are almost laughably far-fetched, there is no doubt that Bach was well aware of some gematric schemes applied to music as well as greatly sensitive to the mathematics of music and numerical relationships in general to sound. There are several lines of evidence for Bach’s mathematical bent beyond his deep understanding of musical tempering. His use of correlations between letters and numbers and the overall numerical symbolism in biblical sequences and musical cryptograms are well-published and only briefly mentioned here with caution, where I would make distinctions between gematria and steganography.
Some background on number play and equivalencies is useful. Gematria is a Hebrew word possibly based on numerology (where alphabet letters have numerical equivalents as in many early arithmetical systems) but is most likely derived from the Greek word for a type of geometry that assigns numerical value to a word or phrase. Similar numerical alphabets use letter and number equivalents or some similar system of representation, some as natural order sequences where every alphabet letter has a direct number equivalent in sequence with values from 1-26 or thereabouts. Other generic systems, like the Greek Milesian alphabet has Alpha to Iota equal numbers 1-10 and Kappa to Tau represent 20-100 in intervals of 10 and Upsilon to Omega represent 200 to 600 in intervals of 100, so not a direct natural order sequence. One of the easiest things to verify about Bach’s familiarity with possible gematria is that one of Bach’s Leipzig librettist collaborators from 1725 onward, Picander (real name Christian Friedrich Henrici 1700-64), was devoted to numerical alphabets. Tatlow and others have demonstrated Bach’s knowledge of Picander’s numerical alphabets was primarily as a genius musician who loved puzzles, musical riddles and number games but also because he was Picander’s friend and collaborator.[4] The name Picander is itself even a numerical pseudonym with numerical gematric value. St. Matthew’s Passion is one of Bach and Picander’s best-known collaborations. [5] Picander compiled his 1718 Paragramma Cabbalisticum Trigonale based on a Milesian alphabet but Bach, like his German contemporary musicians and music theorists Johann Heinichen and Johann Mattheson, is hardly likely to have referenced it primarily for mystic piety or theological reasons, rather using it largely for its possibilities of compounding mathematical invention. That there might be some apparent spiritual symbolism is reasonable but it would not be a driving priority but rather merely allusive or associatively emblematic. But because interpreters like Friedrich Smend took the gematric numerical symbolism too far, any consideration of such deliberate Bach number plays as compellingly normative – like counting measures to come up with symbolic numbers – must proceed with caution, as Malcolm Boyd and others have argued even while accepting his musical play and inventiveness with his name and other devices.[6]
On the other hand, it is unwise to dismiss all number symbolism in Bach because of longstanding biblical precedents in repeated number symbolism, for example, the common biblical repeated use of the symbolic numbers 3, 7 and 12. Bach did impart some theological significance at times in his sacred music. That he often references Trinitarian ideas in ternary relationships between chords and harmonies or use of triplet notes and repetitions of threes in themes and their developments, sometimes with subtle references, is not so arguable. This occurs, for example, with the word Credo (Credo in unam deum) in his 1724 B Minor Mass duplicated 49 (7 x 7) times or the five note toten motif of his 1724 St. John Passion when Christ is handed over to Pilate, symbolizing the commandment “Thou Shalt Not Kill “then repeated ten times in the narrative to symbolize the full Ten Commandments. [7] These are only a few of possible hundreds of numerical codifications to be found in Bach’s music but most are yet to be proven on a one-by-one basis. It must also be remembered that the number of times such repeated words occur in both these major Bach works noted here would be directly from each libretto of Picander rather than from Bach’s music, since the corresponding score depends on the libretto, an important qualification for those looking for added numerical significance in word repetition in Bach.
The mathematics of Bach’s musical tempering is also well-established, although he certainly was not the first to create a logical tempering to please the ear harmonically. [8] In order to avoid what was termed the “wolf or howling tone” the 24 tonalities that depended on pure fifth intervals if perfect Pythagorean tuning was followed, some “tempering” or adjustment had to be made to create tempered fifths across 7 octaves. Bach’s 1722 Well-Tempered Clavier makes ample use of the musical theory necessary to achieve this in his 48 preludes and fugues of the two books, and this same harmonic tempering adjustment occurs in nearly all of Bach’s keyboard music, allowing the performer to play pieces in the full tonalities without having to resort to retuning the keyboard when musical keys were used in different tonalities, especially those considerably removed from the original tonality. [9] This necessary tempering is all the more important given the complexity of Bach’s music, where in his contrapuntal harmony every note is important, no notes are casual or accidental, and even his passing tones establish harmonic progressions and symmetry. Bach’s music may be among the most perfect human creations ever for multiple reasons including its architectonic structure and mathematical complexity.
Some of the more clear examples of Bach’s steganography are more observable, however, in the visual score than to the ear unless one has an ear as subtle as Bach, such as found in the famous use of his name B-A-C-H as a cryptogram, using the note sequence of b flat-a-c-b natural (written as H in German), which is found numerous times in his music, as seen in Bach’s circa 1750 Die Kunst der Fuge (Art of the Fugue, Contrapunctus 19, the last contrapuntal section [10]:
This B-A-C-H theme also appears so frequently elsewhere in Bach it can hardly be coincidental. If possibly gematric in a natural order scheme as some suggest, it can add up to 14 (1+2+3+8) , also expressible as 7 + 7 in a natural order gematria, although Tatlow suggests Bach may have used Picander’s geometric system, which was either Milesian (where it could still add up to 14) or trigonal (not having the same number equivalences as the natural order and instead yielding a different gematric sum of 46, not so immediately meaningful and illustrating how dangerous numerology can be without a consistent key). But possible gematria here are not as important as the steganographic use of Bach’s name. Another famous musical device of Bach depicts itself as an steganographic image of the positions of the crossbars on a crucifixion in his Crucifixus theme for the 1724 B Minor Mass ground bass: 
Perhaps more than anything else and less arguable, Bach’s contrapuntal genius stands on its own as mathematical prowess. The intellectual sophistication of his canons and fugues is at times staggering: not only can pitch and timing change in relation to the number of entries of the fugal subject but also “in timing changes one can find stretto, diminution and augmentation as just a few possibilities” but also inversion, modulation, full key changes and even retrograde or “crab” motion when themes are played backward and / or add alterable elements. That Bach could also perform this kind of difficult composition cold and in public is well-published elsewhere. Hofstader discusses Bach’s 1747 Das Musicalisches Opfer (Musical Offering) with the theme provided by Prussian King Frederick II the Great and Bach’s improvised “impossible” eight part fugue. Even the title is an acrostic word play in Latin: Regis Iussu Cantio Et Reliqua Canonica Arte Resoluta (“At the King’s Command, the Song and Remainder Resolved with Canonic Art”) spelling RICERCAR, an old name for a fugal composition and also meaning a “search” an apt word to describe Bach’s intent for his listeners, [11] as Bach may have been often playful with such “hide-and seek” games in his compositions. In any case, the requisite incredible capacity for complexity in Bach’s mind is mapped out in his music. [12] The musico-mathematical playfulness of steganography and other possible devices would have appealed to a composer as intellectually astute and creative as Bach.
While harmonic ambiguities exist in Bach’s compositions as in all great music, multiple melodic textures leading in different contrapuntal directions all have meaning. The author of this article, Dr. Patrick Hunt, has composed fugues and many examples of contrapuntal music, some of which compositions were premiered at Stanford in 2011. The author knows how difficult it is to create truly contrapuntal music, as heard in a brief live radio link from 2011 (http://www.radio4all.net/index.php/program/50131 , click on red arrow at bottom to play).
It is not unlikely that Bach felt the universe reflected divine harmony even in a contest between the counterpoints of good and evil. If he perceived such order even in the plangent chromatic realities of sometime tragic human affairs and looked beyond to an anticipated heaven, it would be fitting that Bach finished his compositions with SDG, Soli Deo Gloria. That SDG could also be a possibly symbolically gematric device as some wonder may be intriguing and is worth investigating, but in Bach’s case is more likely a statement of humility and marvel at what he saw as God’s creativity.